I am fond of stars, and you? I wouldn’t be mistaken if I say everyone drew a star at least once in their lifetime. Of course, it’s more characteristic for children who draw spaceships flying towards stars or the night sky with stars and the moon; draw a Christmas tree with a star on its top, or their grandfather who passed the war with a star on his chest. Numerous examples can be made of how stars are depicted in children’s art. And adults, I think, draw stars from time to time, why not?
For me a star is, first and foremost, pleasant memories of my childhood: I happened to proudly wear the October Child star on my chest, with Vladimir Lenin’s portrait on it; then to carry a pioneer banner on festivals in the role of a standard-bearer, and the same five-pointed star was on the banner. Well, later on all that went down the drain, and a totally different time began: chewing gums, Cola, other junk; former pioneers turned into businessmen, thieves and politicians; everyone endeavoured to snatch something for themselves, and their share had to be the best. At that, stars became a thing of the past. Yet, occasionally, when man gets outside in the evening, he unintentionally turns his eyes on stars, on those marvellous night creations, and for a moment he forgets about this perishable world and the shares to be snatched, and something greater starts revealing itself to him.
The topic is quite extensive, so I’ve split it into four parts, while the main character in all parts, as you have already guessed, is my favourite sign – the Star.
And I will start the story with a poem, for there is no poetry without stars that inspire so many people.
Silver stars, I shall give my heart to you,
But you should tell me: is it night flowers on which
You shed your radiance, shining perpetually up there?
The silver thoughts of the midnight silence,
You are gentle and spruce at the Fete of Spring.
But what is breathing secretly in you? What dreams do stars have?
The silver waters of heavenly expanse,
What poem are you singing in mirrors of Nature?
The universal lakes! The streams of living waters!
Thus I’ve been silently seeking to weave stars with my heart,
Sighing with my soul near the Milky Way,
And dreaming that I’d find a talisman among amicable stars.
I was asking, I heard an invisible string,
I forgot whether I was looking at Heaven or in my own depth,
But I loved and cherished my love and the Spring.
My soul was trembling of the singing of secret lines,
A mysterious flower unfolded in my soul,
Its name is what I have never been able to find.
But I am full of singing and radiance of strange dreams.
Oh, the fete of betrothal of the Heaven and the petals!
Oh, the sacrament of wedding of constellations and flowers!
Konstantin Balmont
(unrhymed translation of his poem from Russian)
Star: Old English steorra "star," from Proto-Germanic sterron, sternon (source also of Old Saxon sterro, Old Frisian stera, Dutch ster, Old High German sterro, German Stern, Old Norse stjarna, Swedish stjerna, Danish stierne, Gothic stairno). This is from Proto-Indo-European (PIE) ster (source also of Sanskrit star, Hittite shittar, Greek aster, astron, Latin stella, Breton sterenn, Welsh seren). Some suggest it is from a root meaning "to strew, scatter".
In Russian a star is svezda. The original word was gvoizda, literally meaning “shining, luminary” (Old Prussian svāigstan – “radiance, light, glitter”, Old Ossetic zvestæ – “silver”, etc.). – EtymologySchool Dictionary of Russian. The Origin of Words. – Moscow: Drofa, N.M. Shansky, T.A. Bobrova, 2004.
Zvezda: Old Russian звезда (shining, radiance), Proto-Slavonic gvezda (light, glitter). In ancient Rus this word meaning as a “celestial body” was known since the 11th century. Since the 18th century it’s been widely used in poetry, symbolizing something beautiful. An item or image (more often five-pointed) is also called a star: e.g. the Kremlin stars. Kindred words: Polish zwiazda. Derivatives: звездный (stellar, starlit), созвездие (constellation). (Semenov’s Etymology Dictionary of Russian)
“A five-pointed star is also an ancient Slavic symbol discovered in a great number in Gorodets culture settlements. Besides Slavs, five-pointed star images as amulets were used by Finno-Ugric peoples (excavations of the Shatrischensk burial ground near Ryazan: embroidery, badges with a star or with a star and a cross together).”
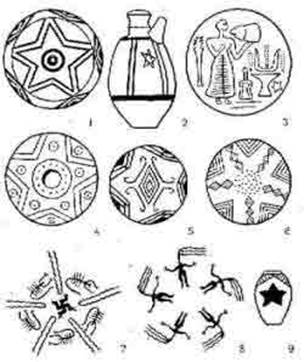
The five-pointed star in ancient times:
1 – Asia Minor, 6 thousand years B.C.
2 – Sumerians, 4 thousand years B.C.
3 – Crete, 3 thousand years B.C.
4 – Troy, 2 thousand years B.C.
5 – Asia Minor, 6 thousand years B.C.
6 – Egypt, 4 thousand years B.C.
7 – North Mesopotamia, 3 thousand years B.C.
8 – Iran, the Later Stone Age
9 – Egypt, the Later Stone Age
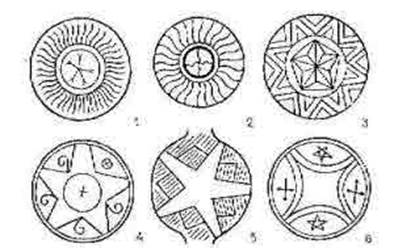
1,2 – Buryat ornament elements
3 – mountainous Georgia
4-6 – North Ossetia, 2-1 thousand years B.C.
Anastasia: Unfortunately... So, regarding the symbols. A crescent, as you have mentioned, was often painted with a star instead of a circle. But the star could be five-pointed, seven-pointed or eight-pointed, which was drawn as either a geometric figure with pointed ledges or simply as rays radiating from the centre.
Rigden: In essence, a star over a crescent is strengthening of what is already strong: this is Allat in Allat. However, such designation is also used as an 
additional indication of one of the powers of Allat. Since ancient times, many-pointed stars have also had their own peculiarities in interpretation of their symbolism. The seven-pointed star is a symbol of the seventh dimension. The eight-pointed star is a symbol of the rhombus (a cube set on one of the corners as a symbol of transformation of man into a spiritual being, entrance into the spiritual world). And the five-pointed star is a working sign associated with the powers of Allat (manifested at the level of the fifth dimension); it belongs to the group of positively working signs. But such subtleties are only understood by people who work with signs in the invisible world.
The sign of the five-pointed star activates a sense of justice and hope for the future in a person (at the subconscious level), and also encourages people to unite. But unfortunately, these unique qualities of the sign have often been used and continue to be exploited by the people serving the Animal Mind. This is, certainly, a weak force compared to the AllatRa sign, but nevertheless, when it’s massively used, it gives a certain result connected with a particular influence on people and change of events in the three-dimensional world. In the case of the five-pointed star, no matter if it is pointing up or down, it will still be a sign of one of the creative powers of Allat. The only question is on what this additional power is spent, or rather, where it is redirected by the people who get it.
Anastasia: Indeed, the five-pointed star has been used since ancient times in different forms of rotation. Its oldest image (if we speak about the artefacts known to this date) is thousands of years old, and it was found in Asia Minor in the culture of which we have already spoken. In the Neolithic era, the sign of the five-pointed star was located above the head of the Great Goddess as her symbol. And among the ancient Egyptians, the five-ray star stood for a “deity.” Images of the five-pointed star above the head of a bull as a sacred animal are known in some ancient beliefs. The sign of this star both with the top pointing down was used as a positive spiritual symbol, containing elements of the Allat sign (the central triangle pointing down as a symbol of the divine creative feminine principle), and with the top pointing up in the same semantic interpretation.
Since ancient times, the star has served as a symbol of victory of the spiritual nature over the material nature. In mythology, it was used to designate the union of Heaven and Earth. This sign was popular among peoples of ancient Europe, Asia (especially the Sumerians and the Persians), America (the aboriginals – the American Indians) and others. And judging by magic rituals of different peoples, it was one of the most commonly used symbols. The sign of the five-pointed star was painted on amulets to protect against the forces of evil. Thanks to the Greek language, this star is known today as the pentagram. In the modern world, the five-pointed star appears as a symbol of many states. Obviously, because the Knowledge was lost, its image began to be interpreted from the human mind in esotericism, and this star with the top pointing up is regarded as a sign of the “White Magician”, while a star pointing down as a sign of the “Black Magician”.
Rigden: Such a division is truly an interpretation from the “human” mind. But it appeared because the creative power of Allat, which is available through this sign, was used for negative purposes. The sign of the star only gives a positive impetus, a surge of energy for a certain change. And where it is later on directed by people is a matter of human choice. Here is a simple example: throughout the history, the sign of the five-pointed star was often used to arrange revolutions and stage coups. The star encouraged a positive surge in the masses, gave motivation, inspired for action while stimulating a yearning for the better in people in terms of their inner disposition. That is why people went towards such transformations in society with faith, a positive attitude, a hope for a better life and future, with a desire to attain the long-awaited freedom. This is exactly the manifested effect of the sign on the masses. But where and for which purpose was all such power redirected by leaders of such coups? Naturally, towards the power of the Animal Mind that substitutes implementation of its material programmes for the notion of people’s spiritual aspirations. So, it turns out that in revolutions and coups people try to overthrow one tyrant in the hope of gaining their own Freedom, but instead they “choose” another tyrant without realizing that nothing of what they expect will change in their lives, and that there will be no Freedom of which every Soul dreams. Such substitutions imposed by the Animal Mind are not understood even by those who stage such mass “shows”, using tremendous human resources (power). People waste their unique power of attention and time to eventually strengthen the power of the Animal Mind in the material world in which they are to live, although for a short time. And the greater the power of the Animal nature is, the more they forget about their Spiritual nature, losing true understanding of the real Freedom and the meaning of their lives. (AllatRa online version, pages 450-453)
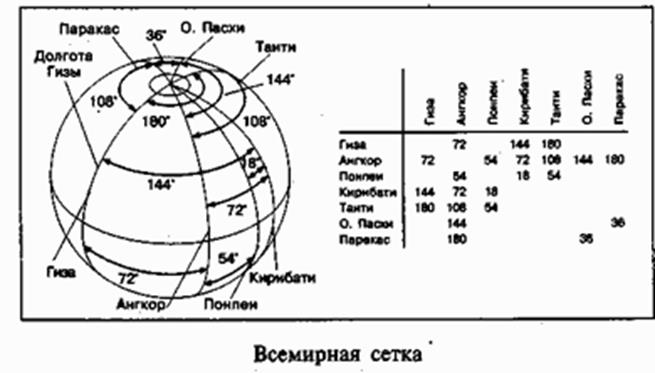
Here’s an interesting chart showing distances in degrees between various interesting places on the planet, where objects of worship are located.
In math, a proportion (Latin proportio) is the equality of two ratios:
a : b = c : d.
A straight line segment AB can be divided into two shares as follows:
The latter is exactly the golden cut (golden section) or cut of the segment in the extreme and mean ratio.
The golden section (golden ratio) is a proportional division of a segment into unequal shares, when the ratio of the entire segment to its bigger share equals to the ratio of the bigger share to the smaller share; or, in other words, the ratio of the shorter segment to the longer one equals to the ratio of the longer segment to the whole:
a : b = b : c
or
c : b = b : a.
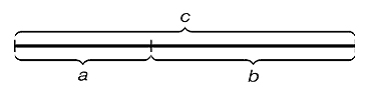
Figure 1. Geometric depiction of the golden ratio
Practical acquaintance with the golden section is usually started with division of a straight line segment according to the golden ratio by means of compasses and a ruler.
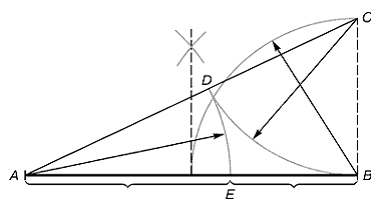
Figure 2. Division of a straight line segment according to the golden ratio. BC = 1/2 AB; CD = BC
From the point B a perpendicular is raised, equal to a half length of the segment AB. A line connects the point C obtained with the point A. On the line obtained a segment equalling to BC is laid, ending in the point D. The segment AD is projected onto the straight line AB. The point E thus obtained divides the segment AB according to the golden ratio.
Golden cut segments are represented in an endless irrational fraction AE = 0.618..., if AB equals to 1, BE = 0.382... For practical purposes, approximate values 0.62 and 0.38 are frequently used. If the segment AB is taken for 100 shares, the longer segment will equal to 62 and the shorter to 38 shares.
Properties of the golden ratio are reflected in the following equation:
x2 – x – 1 = 0.
Solution of the equation:
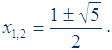
For practical purposes, an approximate value = 1.618 or = 1.62 is used. Rounded at the percentage level, the golden ratio is division of any quantity 62 % to 38 %.
The golden triangle
To determine golden ratio segments of ascending and descending orders, a pentagram can be used.
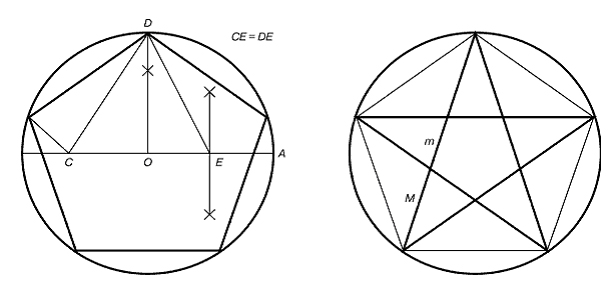
Figure 5. Plotting of a regular pentagon and a pentagram
In order to plot a pentagram it’s necessary to plot a regular pentagon. The method of regular pentagon plotting was developed by German artist Albrecht Dürer (1471-1528). Let’s assume O is a circle centre, A is a point on the circle, and E is the mean point of the OA segment. A perpendicular raised in the point O to the OA radius intersects the circle in the point D. By means of compasses, let’s draw a segment CE = ED on the diameter. The length of the side of the regular pentagon inscribed in the circle equals to DC. Now, let’s lay DC segments on the circle, and we will get five points to inscribe the regular pentagon. Let’s diagonally connect every pentagon vertex with the next nearest one, and we’ll get a pentagram. All pentagon diagonals divide each other into segments that relate to each other according to the golden ratio.
Every corner of the five-pointed star represents a golden triangle, the sides of which form 36° vertex angle, while the triangle base projected onto any of the lateral sides divides it according to the golden ratio.
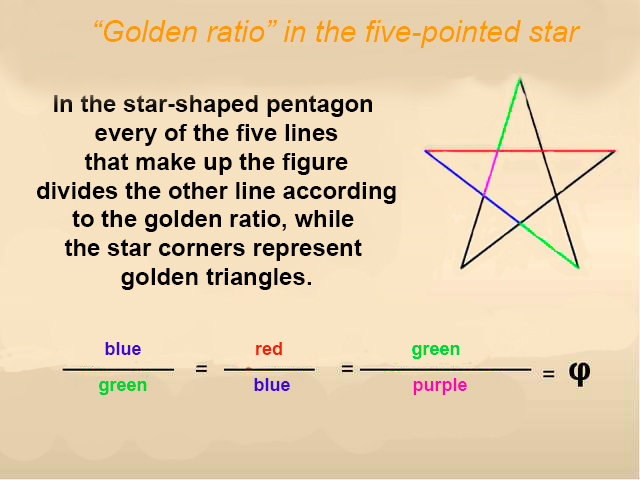
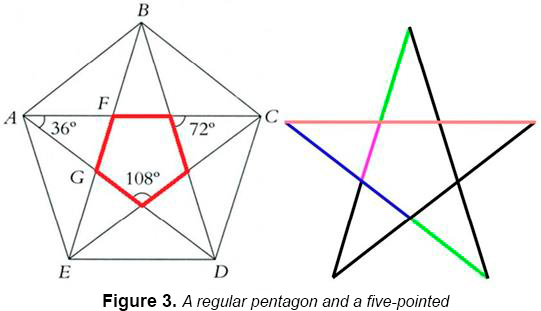
Let’s examine the pentagram, i.e. the star in a circle, and compare it with the chart I gave in the beginning (see the chart, Figure 5 and Figure 3 where the angle values are shown).
We see numbers 36, 72, 108, and the same numbers are noticed in the chart. Now, let’s draw a straight line from any vertex of the star (let’s take the upper one for clearness), which line will divide the circle in half. We will arrive at the following: the star vertex angle equalling to 36 splits into two angles 18 each (the number is in the chart); the line divides the regular pentagon angle of 108 in half, and we get 54 (the number is in the chart), a half of the circle is 180 (the number is in the chart). It turns out the pentagram contains all numbers from the chart, except 144, but 144 is the sum of two angles of 72 degrees each. (The triangle: 72+72+36=180)
The star in a circle or the pentagram as it’s otherwise called proves to be very interesting.
“The thing is that, according to the initial knowledge of Belyao Dzy science, a star is a symbol of the feminine divine principle, whereas a circle means existence, the Universe. A star in a circle means the presence of the feminine divine principle in the circle of existence. Moreover, the feminine principle was regarded as a vessel for reincarnations, and a woman was regarded as the one giving power and life. For this reason ancient Egyptians started using a star inscribed in a circle as a symbol of the kingdom Duat, the kingdom of reincarnation of “human souls.” (Sensei IV book)
It is also interesting that the aforesaid numbers are connected with precession.
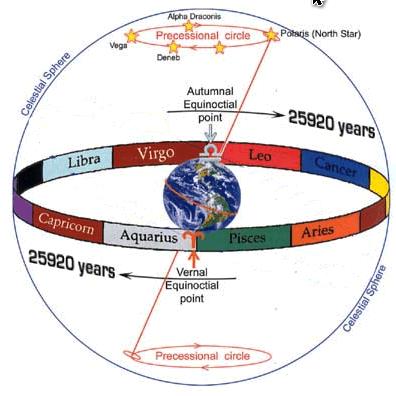
The full precession cycle makes up 25,920 years. If we divide this number by 360, we get 72. It will take 72 years for the earth to pass 1 degree. So, 72 is the principal number. Now, let’s imagine a scale on which there are 2 major units – 0 and 1. One (i.e. one degree) will equal to 72 (in years).
Let’s split our scale into smaller units. 72/2=36 (we will get a half-degree division on the scale), 36/2=18 (a quarter of a degree), 36+18=54 (0.75 degrees or ¾ of a degree).
Let’s extend the scale beyond one: 72+36=108 (1.5 degrees), 108+36=144 (2 degrees), 144+36=180 (2.5 degrees). All these numbers are in the above chart.
We can also obtain number 432 that will equal to 6 on our scale.
An interesting experiment:
Extract from the article What’s behind the Golden Ratio? (Chemistry and Life, No.7, 1988, USSR)
“Homogenate is a suspension of chloroplasts and other cell elements in ordinary water. I prepared it very simply: triturated chopped-up leaves in a mortar with water and filtrated the obtained mixture through fosta nylon cloth. After 12 or more hours of mixture keeping at room temperature, denaturation and sedimentation of homogenate components started. pH of the medium sharply dropped, apparently due to release of Н+ ions by chloroplast membranes that prevailed in the homogenate. Yet, the strange thing was that under identical conditions (temperature, illuminance, homogenate volume, air access, vessel shape) denaturation and sedimentation were often running differently.”
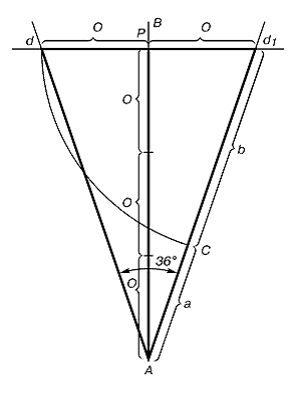
“Homogenate behaviour in vessels placed in a circle was no less amazing. Although everyone knows a circle “has neither beginning nor end”, the speed of homogenate denaturation in several vessels was always higher than in adjacent ones. And it’s noteworthy that the “high-speed” vessels were located in spots corresponding to vertices of a regular pentagon inscribed in a circle (Figure 3), which is so remarkable by its golden proportions. This is the only regular polygon having the 1.618 ratio of its diagonal to its side; at that, each of its diagonals is divided by two other diagonals also according to the golden ratio.
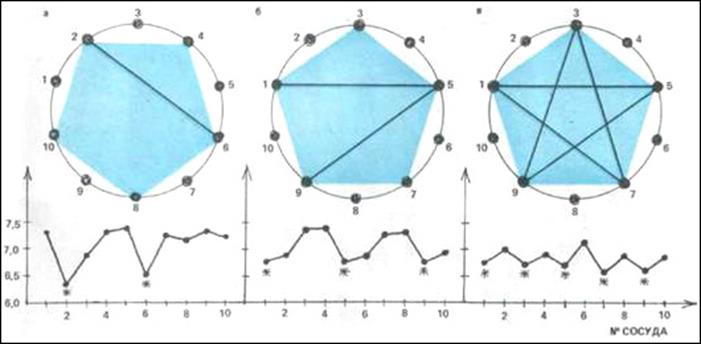
Figure 3. Homogenate denaturation and sedimentation take place faster in the vessels placed in points corresponding to vertices of the regular pentagon inscribed in a circle. There can be two to five of such points.
It turns out the special points which correspond to division of an object (in our experiment it’s a set of vessels or a cuvet) according to the golden ratio or a ratio approximate thereto possess certain peculiar properties? In fact, something in these points runs differently than in adjacent ones.
If you don’t believe, verify yourselves.”
M.S. RADIUK,
Institute of Photobiology of the BelorussianSSRAcademy of Sciences
“Knowing what takes place in the invisible world when two elementary particles collide, it gets clear why same reactions (with identical external conditions) are in fact never absolutely identical, and there are always minor fluctuations in them.”
PRIMORDIAL ALLATRA PHYSICS
I also recommend readers to look through articles here: http://allatra-science.org/
In particular:
http://allatra-science.org/publication/allat-i-neutron
http://allatra-science.org/publication/nejtrino-i-zolotoe-sechenie
To be continued.
Prepared by Igor
Star. The Golden Ratio (Part 1)
votes:
375
|
02.08.2017
10.07.2016
25.07.2016
31.07.2016
Project Aim
Leave comment