‘Underlying all Egyptian speculation’, as R. T. Rundle Clark has observed, ‘is the belief that time is composed of recurrent cycles which are divinely appointed ...’ There is furthermore a governing moment amongst all these cycles and epochs – the ‘genesis event’ that the Egyptians called Zep Tepi, the ‘First Time’. (Graham Hancock, Robert Bauval. THE MESSAGE OF THE SPHINX, or KEEPER OF GENESIS)
‘Many believe the Pyramid Age is the time when Giza pyramids were created, the time of a single special dynasty or group of pharaohs. However, the plan was much more grandiose and was not limited to the Fourth Dynasty’s creations. There are plenty of evidence leading to conclusion that there was a single great plan ‘to freeze the time’ in stone or in other words to make stones ‘tell’ about the ‘First Time’.’ (Robert Bauval. The Orion Mystery: Unlocking the Secrets of the Pyramids)
***
Please, review the previous articles on the subject:
***
‘There is, however, another science which, provided one essential precondition is fulfilled, can provide a much more accurate dating – to within a few decades – of uninscribed ancient stone monuments. This is the science of archaeoastronomy. The precondition upon which it depends for its successful functioning is that the monuments studied should have been accurately aligned to the stars or to the rising points of the sun by their builders.
The Great Sphinx fulfils this precondition. It lies exactly along the east-west axis of the Giza necropolis with its patient and eternal gaze set perfectly towards due east. It is, therefore, a superb ‘equinoctial marker’: its eyes target the exact position of sunrise at dawn on the spring equinox.
To clarify matters a little, astronomers speak of four ‘cardinal moments’ in the year: the summer solstice – the longest day in the northern hemisphere – when the earth’s north pole points most directly at the sun, the winter solstice, the shortest day, when the pole points most directly away from the sun, and the spring and autumn equinoxes when the earth lies broadside-on to the sun and when night and day are of equal length.
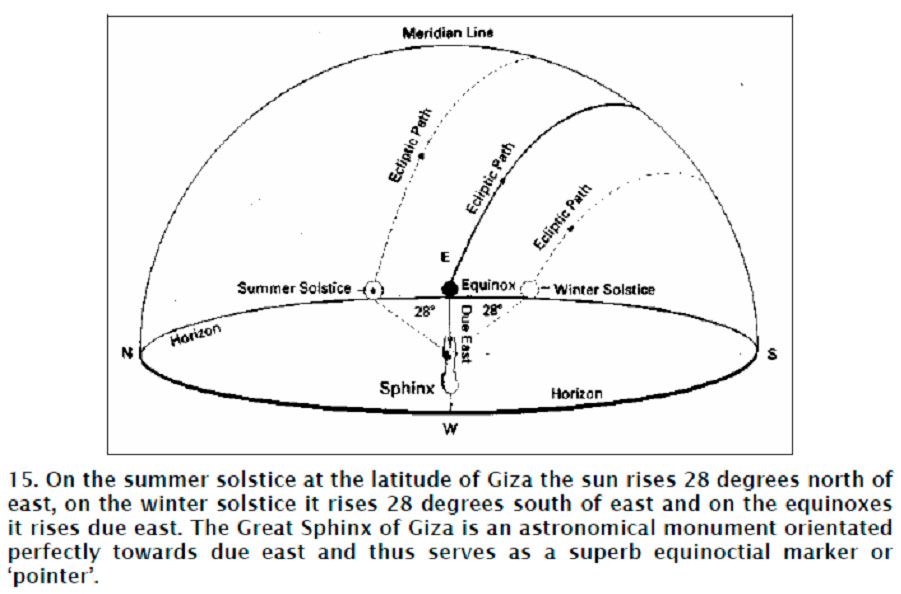
On the summer solstice at the latitude of Giza, the sun rises about 28 degrees north of east. On the winter solstice it rises about 28 degrees south of east. By contrast, the main characteristic of the equinoxes (here and everywhere else around the globe) is that the sun always rises due east providing a sure and accurate geodetic reference to one of the cardinal directions.
It is towards this reference point, with high precision, that the gaze of the Sphinx is set – not by accident, but by design, and as part of a vast, archaic astronomical plan of uncanny accuracy and intelligence.’

In Sensei of Shambala (Book IV) the Great Sphinx’s role in the ancient astronomical plan is mentioned twice. It actually plays the main, paramount role in the literal sense of the word.
Here are relevant quotes from Sensei of Shambala (Book IV):
‘The place chosen by Imhotep for construction of this truncated pyramid wasn’t occasional. It was on the verge of the plateau, that very plateau which was only a few kilometres to the north of the Great Sphinx. When Imhotep showed the site layout to the pharaoh, priests and aristocrats, he explained the choice of this place of deserted plateau as a closer location to Memphis and a beautiful view from that place on Memphis. But in actual fact this place fully matched one of the earth geographical coordinates marked on the ‘star map’ revealed to him by the Sokrovennik. The Great Sphinx erected far earlier than that time (and not after Imhotep’s life as they assume it now, as if it were during the time when the Great Pyramids were built!) was an important reference point for precise and accurate location of the truncated pyramid.’
‘Right you are, the pharaohs Khufu, Khaef-ra and Men-kau-ra,’ Sensei nodded with satisfied air. ‘By the way, namely these pyramids were built according to the drafts of Imhotep by his disciples in compliance with precise coordinates on the ‘star map’. And, as I have already said, the Great Sphinx was the main reference point for this.’
Let me proceed to the theory: source.
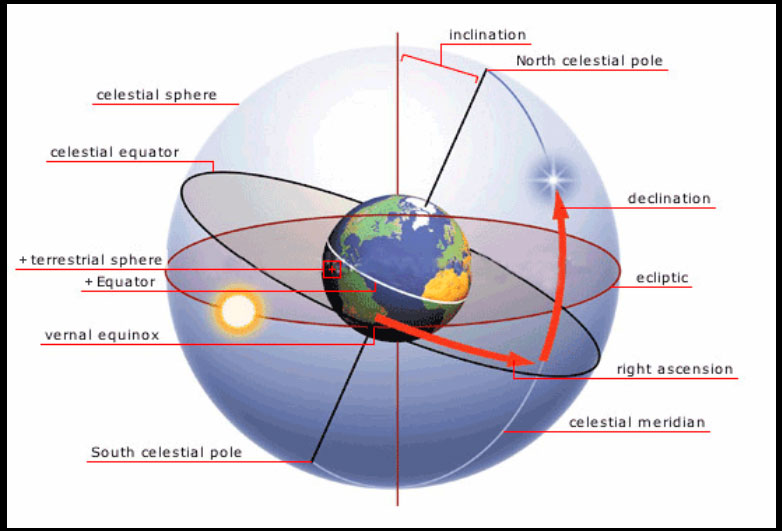
To find stars in the sky, compose star maps, determine time and geographic coordinates, one should know coordinates of relevant stars.
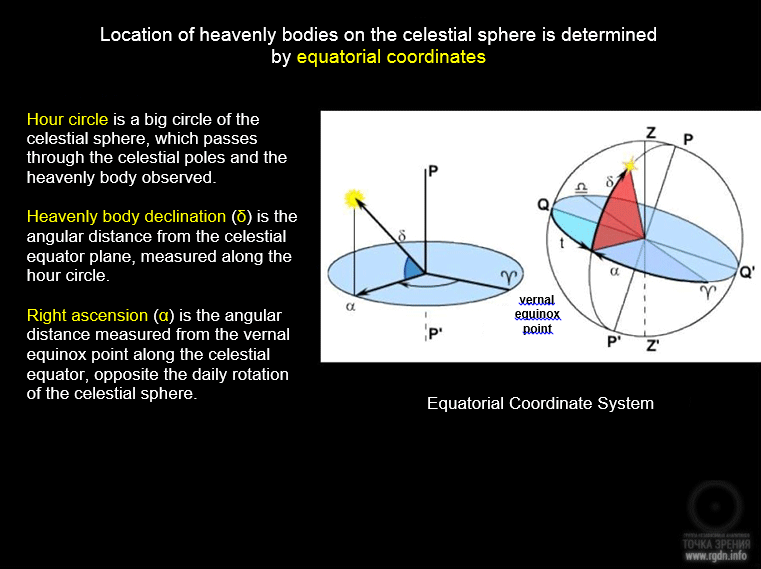
For this the equatorial coordinate system is applied, which is similar to the geographic coordinate system on the globe (see image below). We can estimate locations of stars in degrees on the celestial sphere relative to the celestial equator, just like we estimate angular distances from various cities to the terrestrial equator on a globe or world map (such distance is called the geographic latitude). The angular distance from heavenly bodies to the celestial equator is called declination. Declinations marked with the lower-case letter Delta (δ) in the southern hemisphere of the celestial sphere are considered negative.
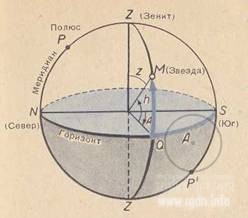
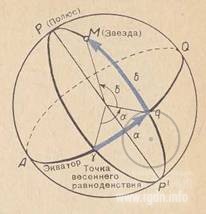
Coordinate systems. Left – relative to the horizon; height h and azimuth A; right – relative to the celestial equator: right ascension Alpha and declination Delta.
The second geographic coordinate on the Earth is the longitude – an angle between the plane of the meridian in a given place and the plane of the prime meridian. On the celestial sphere, the second coordinate is the right ascension – an angle between the plane of a semicircle drawn from the celestial pole through a heavenly body (the hour circle) and the plane of a circle drawn from the celestial pole through the vernal equinox point on the equator (the prime hour circle). This point is called so because the Sun is in it on the celestial sphere on 21 March, when the day equals to the night. The right ascension marked with the letter Alpha (α) is estimated from the vernal equinox point counter-clockwise, i.e. towards the sky daily rotation. It’s convenient to express both the geographic longitude and the right ascension not in degrees, but rather in time units, for within 24 hours the Earth and, as it seems to us, the sky do one turn on the axis. Hence, we get the following ratio:
360° correspond to 24 hours
15° Ø 1 hour
1° Ø 4 minutes of time
15’ Ø 1 minute of time
15” Ø 1 second of time
For example, the geographic longitude or right ascension of 3 hours 10 min. 20 sec. makes 47°35'00". It’s easy to understand stars culminate one after another along with the increase of their right ascension.
Declination and right ascension (Alpha and Delta) are called the equatorial coordinates. For stars they change so slowly that we may consider them invariable, unless we need a special precision. While the celestial sphere daily rotates, the vernal equinox point rotates along with it. Thus, locations of stars relative to the equator and the vernal equinox point depend neither on the time of the day nor on the observer’s place on the Earth. Addendum IV contains a list of Alpha and Delta coordinates for several bright stars. The same coordinate grid is depicted on the interactive night sky map. The Sun, the Moon and the planets permanently move against the star background. Therefore, they are not depicted on the map (their coordinates on each day of the year are published in special astronomical calendars).
Upon daily rotation of the celestial sphere location of stars relative to the celestial equator does not change. Therefore, equatorial coordinates are used for drawing of star maps and atlases.

Furthermore, it should be emphasized the Great Sphinx ‘was an important reference point for precise and accurate location of the truncated pyramid’. This is true for any pyramid built by the star map possessed by Imhotep. No matter in which part of the globe a pyramid was constructed, it was necessary to know the accurate distance from the Great Sphinx to the geographic region of the pyramid placement. In this respect, there is an interesting quotation which we’ve already cited in the article Navels of the World and the Soul of the Mother of Stars:
Because of the advanced geodetic and geographic science of the Egyptians, Egypt became the geodetic centre of the known world. Other countries located their shrines and capital cities in terms of the Egyptian ‘zero’ meridian, including such capitals as Nimrod, Sardis, Susa, Persepolis, and apparently even the ancient Chinese capital of An-Yang… As each of these geodetic centres was a political as well as a geographical ‘navel’ of the world, an omphalos, or stone navel, was placed there to represent the northern hemisphere from equator to pole, marked out with meridians and parallels, showing the direction and distance of other such navels.
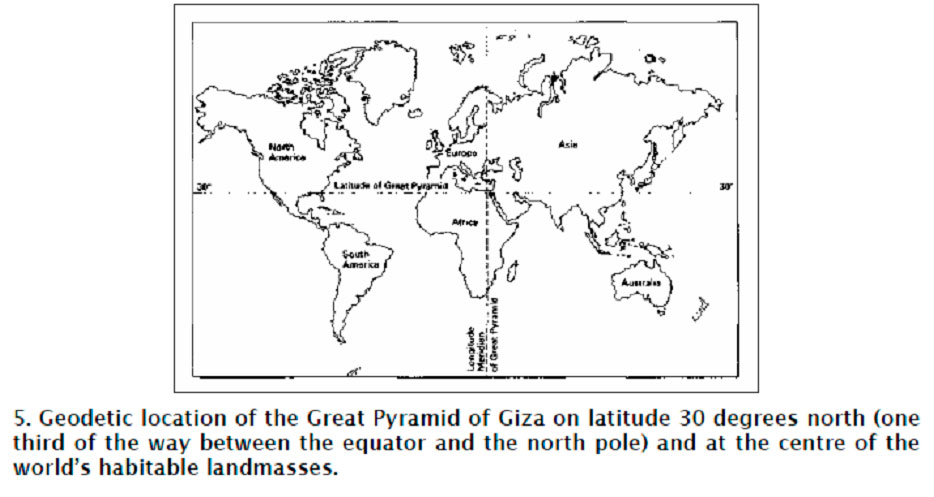
For some reason the authors of the above quote don’t take into account Egypt was not only the centre of geodesy and geography, but the unquestionable centre of astronomy and observation of stars as well, whereas the first so-called navel was the Giza plateau or more specifically the Great Sphinx. Should we look on the map, we can see Giza being almost at the centre of the world’s habitable landmasses.
‘The vast cosmic engine of the earth’s axial wobble offers us a mechanism by which this can be done: we need only instruct our computer to track the precessionally induced movements of the stars backwards in time.
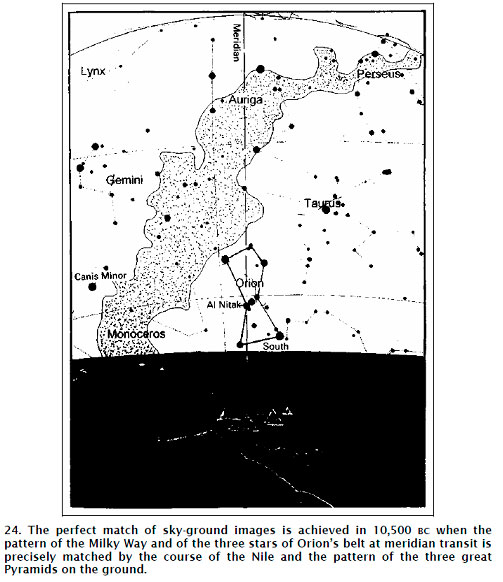
As it does so, millennium by millennium, we observe that the orientation of Orion’s belt at culmination is slowly rotating anti-clockwise and thus approaching ever closer to our desired meridian-to-meridian match. It is not until 10,500 BC, however – 8000 years before the ‘Pyramid Age’ – that the perfect correlation is finally achieved with the Nile mirroring the Milky Way and with the three Pyramids and the belt stars identically disposed in relation to the meridian.
There is a feature of this 10,500 BC correlation which suggests strongly that coincidence is not involved. The pattern that is frozen into monumental architecture in the form of the Pyramids marks a very significant moment in the 25,920-year precessional cycle of the three stars of Orion’s belt – one that is unlikely to have been randomly selected by the Pyramid builders.
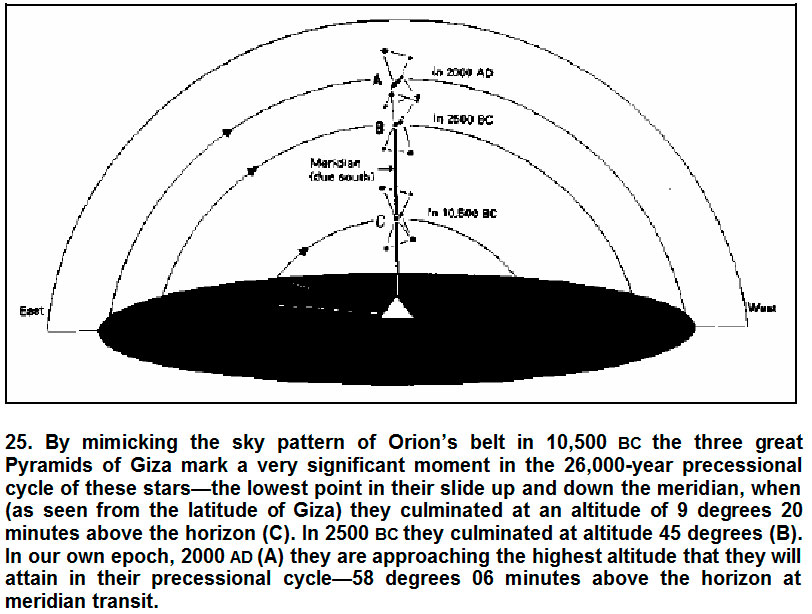
To get a clear grasp of what is involved here let us call up a computer simulation of the skies over Giza in our own epoch, circa AD 2000. Looking due south we note that Al Nitak crosses the meridian at an altitude of 58 degrees 06’ above the horizon. This, as it happens, is within 8 minutes of the highest altitude that this star will attain in its precessional cycle, i.e. 58 degrees 14’ (to be reached at around AD
2500).
Let us now project our simulation backwards in time and recreate the sky as we would see it if we were standing in the same position at around 10,500 BC – i.e. just under 13,000 years, or half a precessional cycle, earlier. In this remote epoch we discover that Al Nitak crosses the meridian at an altitude of only 9 degrees 20’ above the horizon. [11 – Using the rigorous formula of precession corrected for nutation, aberration of starlight, proper motion (from the most recent Yale Bright Star Catalog) and parallax, gives circa 10,500 BC as the epoch that Orion’s belt reached its lowest altitude (9 degrees 25’ measured at the south meridian, i.e. declination 50 degrees 35’), which corresponds to the 25,920-year precessional cycle.]
It will never fall lower, the epoch of 10,500 BC marks the nadir of the star’s precessionally induced slide up and down the meridian (just as the epoch of AD 2500 marks its zenith). Like a slowly moving lever in a narrow vertical slot, it takes 12,960 years to descend from top to bottom, and a further 12,960 years to ascend from bottom to top again.
By exactly mimicking the disposition of the belt stars in the sky in 10,500 BC the layout of the Pyramids on the ground thus not only signifies a specific epoch but also rather precisely and surgically marks the beginning of a precessional half-cycle.’
‘As was pointed out in Fingerprints of the Gods, the same role is played by the Great Sphinx – which gazes directly at the equinoctial rising point of the sun in any and every epoch, past, present and future, forever.
This orientation provides us with an astronomical basis for dating the monument because it is known that the attention of astronomers in ancient times was particularly focused on the zodiacal constellation – considered to define the astrological ‘Age’ – that rose just ahead of the sun in the eastern sky at dawn on the spring equinox. The same phenomenon of the earth’s axial precession that affects the altitude of stars at the meridian also affects these famous constellations – Leo, Cancer, Gemini, Taurus, Aries, Pisces, Aquarius, etc. – the coordinates of which, in relation to the rising point of the equinoctial sun, undergo slow but continuous precessionally induced changes. The result is a hard-to-observe astronomical phenomenon, known as the precession of the equinoxes, which manifests as a gradual circulation of the equinoctial point around all twelve ‘houses’ of the zodiac. In the words of historians of science Giorgio de Santillana and Hertha von Dechend, whose essay Hamlet’s Millis a ground-breaking study of archaic precessional mythology:
‘The constellation that rose in the east just before the sun (that is, rose heliacally) marked the ‘place’ where the sun rested ... It was known as the sun’s ‘carrier’, and as the main ‘pillar’ of the sky. ... The sun’s position among the constellations at the vernal [spring] equinox was the pointer that indicated the ‘hours’ of the precessional cycle – very long hours indeed, the equinoctial sun occupying each zodiacal constellation for just under 2200 years.’
In our own epoch the sun on the spring equinox rises against the stellar background of the constellation of Pisces, as it has done for approximately the last 2000 years. The ‘Age of Pisces’, however, is now approaching its end and the vernal sun will soon pass out of the sector of the Fishes and begin to rise against the new background of Aquarius. To be precise, it takes exactly 2160 years for the equinoctial point to pass completely through one constellation or ‘house’ of the zodiac.
With this process in mind, let us now reverse Santillana and von Dechend’s ‘precessional clock’. Passing back through the Age of Pisces (and the Age of Aries that preceded it) we find that in the epoch of 2500 BC, when the Sphinx is conventionally assumed to have been built, it was the constellation of Taurus that housed the sun on the spring equinox.
It is here that the crux of the problem lies. To state the case briefly:
1. The Sphinx, as we have seen, is an equinoctial marker – or ‘pointer’.
2. On a site that is as profoundly astronomical as Giza one would naturally expect an equinoctial monument dating from the ‘Age of Taurus’ either to have been built in the shape of a bull, or at any rate to symbolize a bull. The Sphinx, however, is emphatically leoninein form.
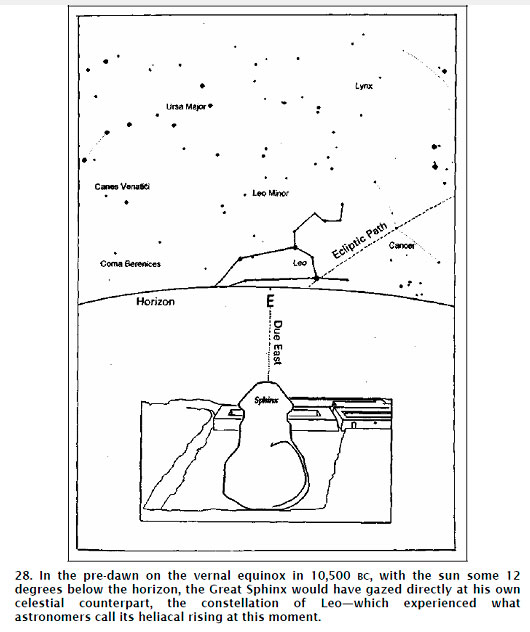
3. It is a simple fact of precession that one must go back to the ‘Age of Leo’ beginning at around 10,500 BC, in order to obtain the ‘correct’ sky-ground symbolism. This, as it turns out, is the only epoch in which the due-east-facing Sphinx would have manifested exactly the right symbolic alignment on exactly the right day – watching the vernal sun rising in the dawn sky against the background of his own celestial counterpart.
To clarify this latter notion, let us return to our computer simulation of the skies over Giza in 10,500 BC, instructing the program to recreate the positions of the sun and stars just before dawn on the spring equinox in that epoch. And let us set our direction of view due east in line with the gaze of the Sphinx. Indeed, with the aid of a little virtual reality and poetic license, let us imagine that we are standing between the paws of the Sphinx itself at that date – a date that we already know accords rather well with the geologyof the monument.
What we would see, occupying the portion of the sky into which the sun is about to rise, would be the splendid zodiacal constellation of Leo – a constellation that very strongly resembles its namesake the lion and thus also the leonine Sphinx.
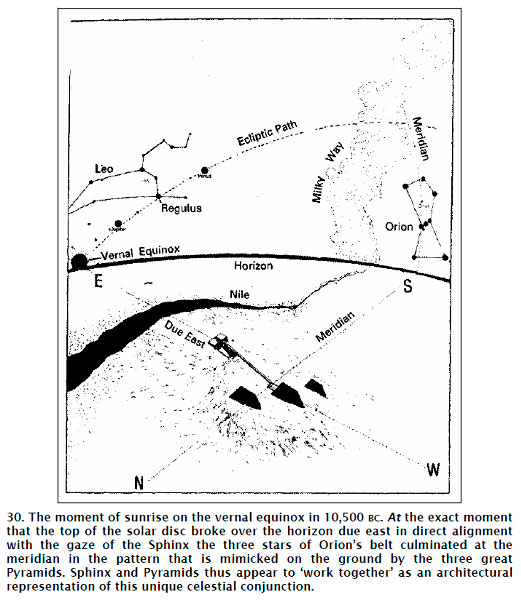
The minutes pass. The sky begins to lighten. Then, at the exact moment at which the top of the solar disc breaks over the horizon directly ahead of us we make a 90-degree right turn – so that we are now looking due south. There, culminating at the meridian at altitude 9 degrees 20’, we observe the three stars of Orion’s belt forming a pattern in the sky that is identical to the ground plan of the Giza Pyramids.
The question reduces to this: is it a coincidence, or more than a coincidence, that the Giza necropolis as it has reached us today out of the darkness of antiquity is still dominated by a huge equinoctial lion statue at the east of its ‘horizon’ and by three gigantic Pyramids disposed about its meridian in the distinctive manner of the three stars of Orion’s belt in 10,500 BC?
And is it also a coincidence that the monuments in this amazing astronomical theme park manage to work together – almost as though geared like the cog-wheels of a clock – to tell the same ‘time’?
Throughout the ancient world the moment of sunrise, and its conjunction with other celestial events, was always considered to be of great importance. At the spring equinox in 10,500 BC, as should by now be obvious, a particularly spectacular and statistically improbable conjunction took place – a conjunction involving the moment of sunrise, the constellation of Leo and the meridian transit of the three stars of Orion’s belt. It is this unique celestial conjunction (which furthermore marks the beginningof the ‘Age of Leo’ and the beginningof the upwards precessional cycle of the belt stars) that the Great Sphinx and the three Pyramids of Giza appear to model.’
‘Another bit of the 10,500 BC ‘jackpot of correspondences’ concerns the star Sirius, which symbolizes the very heart of the ancient Egyptian mystery.
All stars, including our own sun (and our solar system with it) move through space. Because of the vast distances involved, however (hundreds and often thousands of light-years), this ‘proper motion’ registers barely perceptible effects on the positions in the skyof the majority of stars as viewed from earth. Where these stars are concerned the only significant factor is precession (which, as we know, is a perceived ‘motion’ that is actually caused by a wobble on the axis of the earth).
Sirius is one of the major exceptions to this rule. As many readers will be aware, it is the brightest star in the sky. It is also one of the neareststars to earth, being only 8.4 light-years away. Because of this proximity it registers a very large ‘proper motion’ in space relative to our own solar system – large enough to bring about observable changes in its celestial address, over and above those caused by precession, within just a few thousand years.
To be specific about this, the proper motion of Sirius is estimated to be in the range of 1.21 arc-seconds per year (about 1 degree every 3000 years). This means that for an epoch as far back as 10,500 BC, the change in its celestial co-ordinates resulting from proper motion could exceed 3 full degrees of arc, i.e. about six times the apparent diameter of the moon. [Sirius has a proper motion of 1.21 arc seconds per year. For 13,000 years this would give 4.36 degrees of motion. But the motion is oblique to the meridian, giving some 3 degrees decrease in declination.]
Once this rapid and noticeable rate of movement is taken into account alongside the effects of precession, computer simulations indicate a rather intriguing state of affairs. Calculations show that when Sirius reached its ‘First Time’ – i.e. its lowest altitude above the horizon – viewers at the latitude of Giza (30 degrees north) would have seen it resting exactly on the horizon. Moreover it was from this latitude, and this latitude only, that such a conjunction of star and horizon could be witnessed. [Calculations using the rigorous formula for precession corrected for nutation, aberration of starlight, proper motion (from the most recent Yale Bright Star Catalogue) and parallax was done by astronomer Adrian Ashford in August 1995. In circa11,850 BC Sirius would theoretically be at the lowest point in its cycle, with a declination of -60 degrees, thus just on the south horizon. In 10,500 BC it would have had a declination of nearly -59 degrees, thus shining brightly approximately 1 degree over the south horizon as seen from Giza.] The implication is that a special co-relationship exists between the latitude of Giza and the star Sirius at its ‘First Time’.’

In 10,500 BC quite an interesting and beautiful picture could be observed in the starry sky at the latitude of Giza.
“Four ways will appear before their eyes.
Three are false, those are ways of Druj’s helpers,
And devas will push people there, to the dark pit.
The fourth is the way of Arta, way of Spirit and Truth,
That path leads over the abyss.
Slavic brave people will glorify themselves,
Seeing such way that leads to salvation.
Good fortune will be granted to people.
And soon for their courage and truth
They will be rewarded with richness of Soul
And might of material things.
The world will split into two parts.
Malicious will remain behind
With devas, Druj’s servants.
Nature will turn most of them into dust.
They are the end of the end.
Righteous will step side by side with Slavs,
Having made their choice in thoughts, words and deeds.
They will lay the Beginning from the end…”
‘In 10,500 BC the star Al Nitak in the belt of Orion was at the lowest altitude of its precessional cycle and Leo housed the vernal-equinox point. In our own epoch – the epoch of AD 2000 – the other extreme of the curious ‘balancing mechanism’ of Giza is about to be reached: Al Nitak today stands within a few arc seconds of the highest altitude that it will attain in its precessional cycle and the vernal point is about to drift into the constellation of Aquarius. Between the ‘First Time’ and the ‘Last Time’, in other words, the skies have reversed themselves – literally flipped left to right – with Aquarius now marking the vernal equinox and Leo marking the autumnal equinox.’
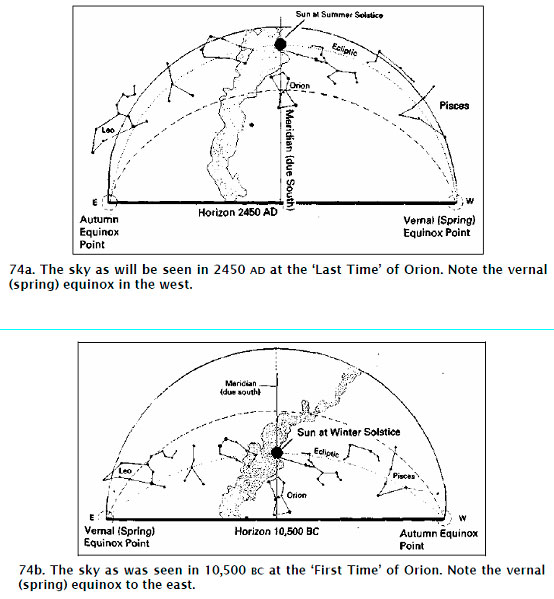
As indicated above, ‘Between the ‘First Time’ and the ‘Last Time’, in other words, the skies have reversed themselves.’
Let’s dwell on this point at greater length. Please, look at the two images above more attentively, in particular at the vernal equinox point on 74a and 74b.
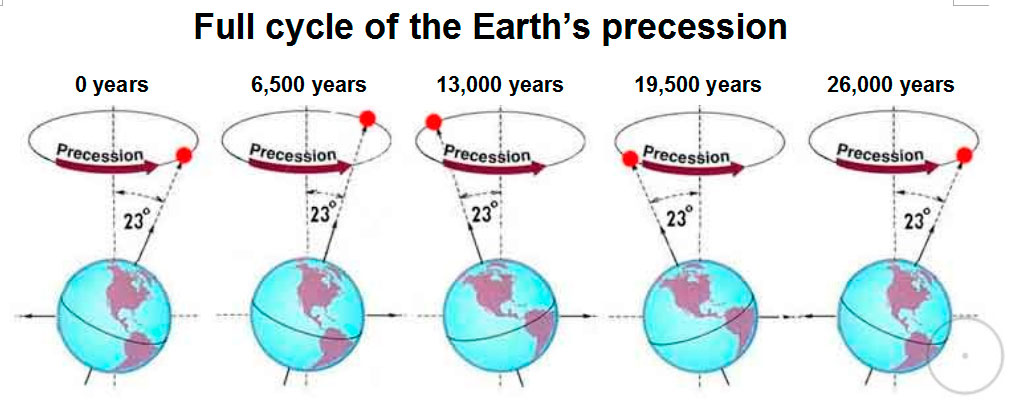
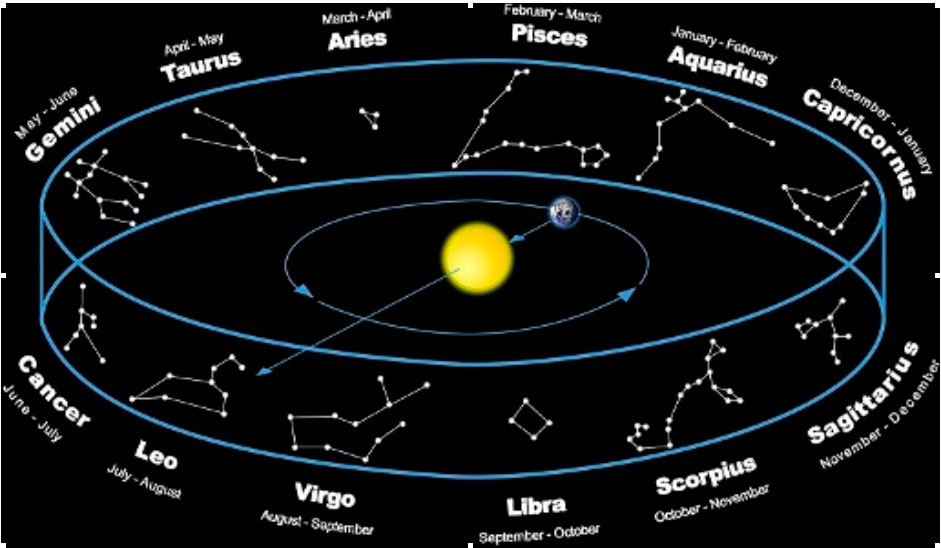
Approximately every 2160 years, as the above information indicates, on the vernal equinox our Sun rises in a different zodiac constellation. We call it the Age, e.g. the Age of Pisces or the Age of Aquarius. The full cycle is 2160*12 = 25,920 years.
The First Time: 12,500 years ago on the vernal equinox the Sun rose in the constellation of Leo, and that was the Age of Leo, while the constellation of Aquarius was in the west then, and the Sun set in it.
The Last Time: On the vernal equinox the Sun rises in the east, in the constellation of Aquarius now, i.e. in the same constellation where during the First Time the Sun set in the west. Therefore, relative to the First Time the Sun now rises in the west.
A cycle begins and a cycle ends – for stars and planets, for people and civilizations. As Zarathustra said:
You are sagacious, Wise friend,
Let your generous gifts that we deserve descend on us,
May Ahura’s Will be done!
To be continued…
Prepared by Igor
 Keeper of Genesis. Part III. The First Time. The Last Time
votes:
214
Keeper of Genesis. Part III. The First Time. The Last Time
votes:
214
|

Project Aim










Leave comment